

Therefore use equation (24.4) to substitute for y2. This gives a second-order equation but one that still depends on y2. To transform the system into a second-order differential equation, differentiate equation (24.3) to get y, = «11 v | -F any.
#Difference equation systems how to
Since we already know how to solve a linear, second-order differential equation, this procedure provides an easy way to rind the solution. It is possible to convert this system of two first-order differential equations into a single second-order differential equation using a combination of differentiation and substitution. The homogeneous form of the system of two linear, first-order differential equations (24.1) and (24.2) is This is done by setting the terms in each equation equal to zero. The first step in obtaining a complete solution is to put lite differential equation system into its homogeneous form. and yf is the particular solution for y.ĭefinition 24.2 The General Solution to the Homogeneous Forms v, is the complete solution, yj' is the general homogeneous solution for y. The complete solutions are the sum of the homogeneous and particular solutions. The equations must be solved simultaneously because y, depends on the solution for y2 and y: depends on the solution for y(.Īs in previous chapters on linear differential and difference equations, we separate the problem of finding the complete solutions into two parts We first y, = «ii.vi +any2 +įind the homogeneous solutions and then find particular solutions. The system is autonomous because the coefficients. The system is linear because it contains only linear differential equations which, as usual, means that y, and vf arc not raised to any power other than one. This method is suited to solving a differential equation system consisting of exactly two linear differential equations.Ī linear system of two autonomous differential equations is expressed as We then proceed to a more general method, known as the direct method, that can be used to solve a system of linear differential equations with more than two equations. We begin with the simplest case-a system of two linear differential equations- and solve it using the substitution method. 24.1 Linear Differential Equation Systems The purpose of this chapter is to extend our single equation techniques to solve systems of autonomous differential and difference equations. When the model is dynamic and involves two or more variables, a system of differential or difference equations arises.
#Difference equation systems series
Dynamics of Continuous, Discrete and Impulsive Systems, Series A Mathematical Analysis 2006, 13: 499–507.It is common in economic models for two or more variables to be determined simultaneously.
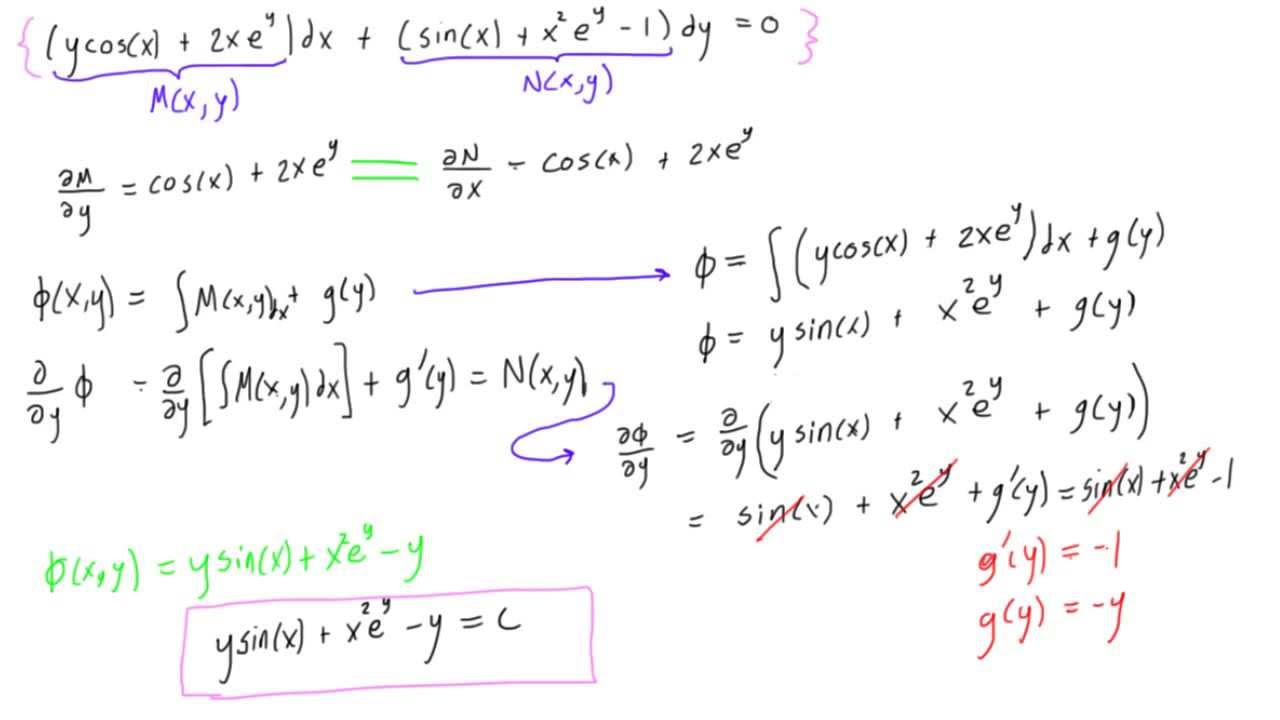
Irićanin B, Stević S: Some systems of nonlinear difference equations of higher order with periodic solutions. Advances in Difference Equations 2007, 2007:-13. Papaschinopoulos G, Schinas CJ, Stefanidou G: On a -order system of lyness-type difference equations. Differential Equations and Dynamical Systems 1999, 7(2):181–196. Papaschinopoulos G, Schinas CJ: Invariants for systems of two nonlinear difference equations. Communications on Applied Nonlinear Analysis 1998, 5(2):47–59. It turns out that many linear systems of differential equations. Papaschinopoulos G, Schinas CJ: On the behavior of the solutions of a system of two nonlinear difference equations. This invariance of the coordinate axes for uncoupled systems follows directly from (). Özban AY: On the system of rational difference equations, Applied Mathematics and Computation 2007, 188(1):833–837. Özban AY: On the positive solutions of the system of rational difference equations, Journal of Mathematical Analysis and Applications 2006, 323(1):26–32. Communications on Applied Nonlinear Analysis 2001, 8(1):1–25.

Grove EA, Ladas G, McGrath LC, Teixeira CT: Existence and behavior of solutions of a rational system. Çinar C, Yalçinkaya İ: On the positive solutions of difference equation system, , International Mathematical Journal 2004, 5(5):521–524.Ĭlark D, Kulenović MRS: A coupled system of rational difference equations.
Çinar C: On the positive solutions of the difference equation system, Applied Mathematics and Computation 2004, 158(2):303–305. 10.1006/jmaa.1997.5829Ĭamouzis E, Papaschinopoulos G: Global asymptotic behavior of positive solutions on the system of rational difference equations. Journal of Mathematical Analysis and Applications 1998, 219(2):415–426. Papaschinopoulos G, Schinas CJ: On a system of two nonlinear difference equations.


 0 kommentar(er)
0 kommentar(er)
